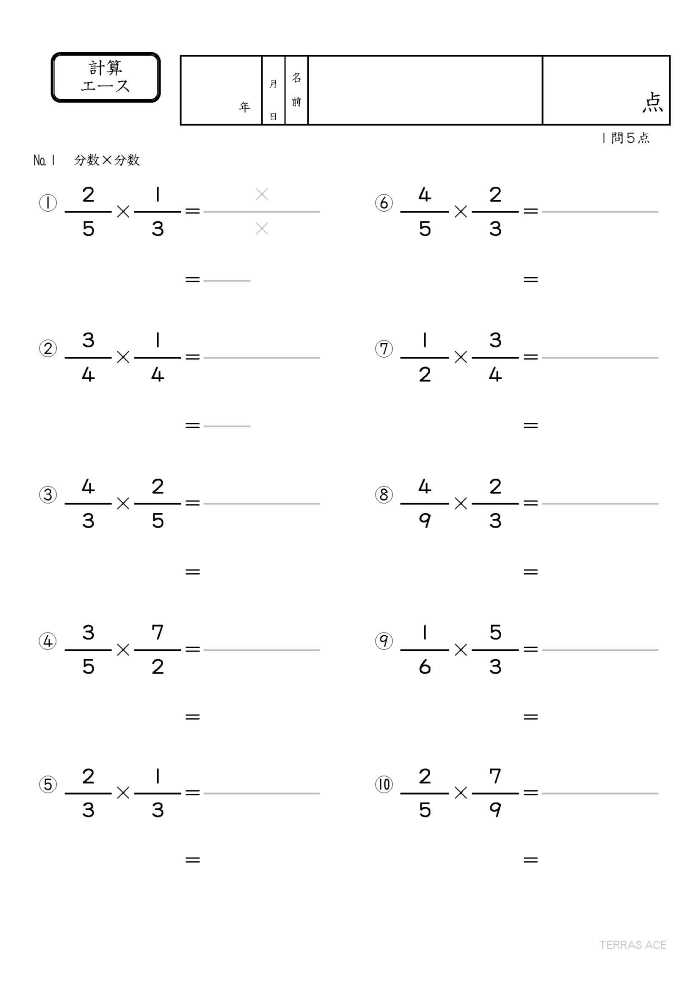
6年生の計算について
6年生の算数の主な計算領域は
・分数×整数、分数÷整数
・分数×分数
・分数÷分数
です。
5年生で学習する通分の必要な分数のたし算ひき算よりも、ルールをしっかり守れば計算しやすい内容です。
ルールを理解するためにしくみをみていきます。
分数×整数の計算のしくみは
例えば
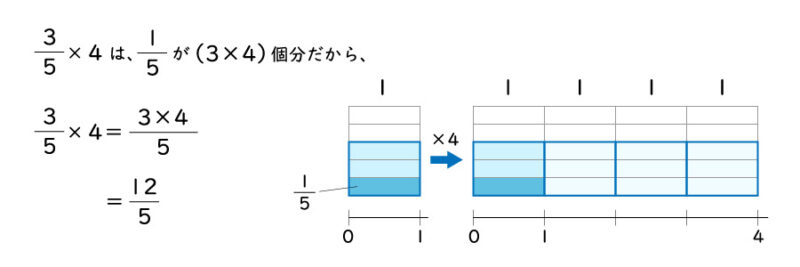
となり、分母はそのままで、分子にその整数をかけるというルールが成り立ちます。
$\frac{b}{a} \times c = \frac{b \times c}{a}$
かけ算のしくみはわかりやすいのですが、
少しわかりづらいのがわり算です。
分数÷整数の計算のしくみは、
例えば
$\frac{4}{5} \div {3}$は、
1を5つにわけていたものをさらに3等分すると全部で15等分になり、そのうちの4つ分ということになります。
つまり、
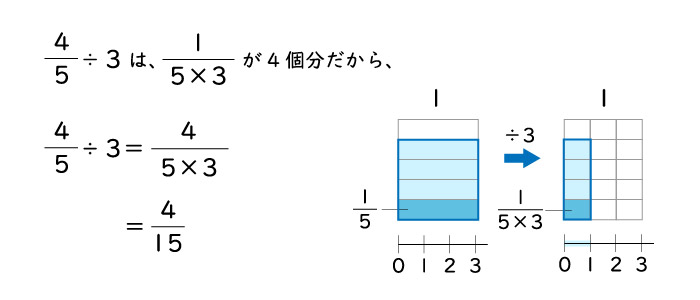
分数÷整数では、分子のそのままで、分母にその整数をかけるというルールが成り立ちます。
$\frac{b}{a} \div c = \frac{b}{a \times c} $
つぎに分数×分数は、上記の分数×整数、分数÷整数のルールを利用すると
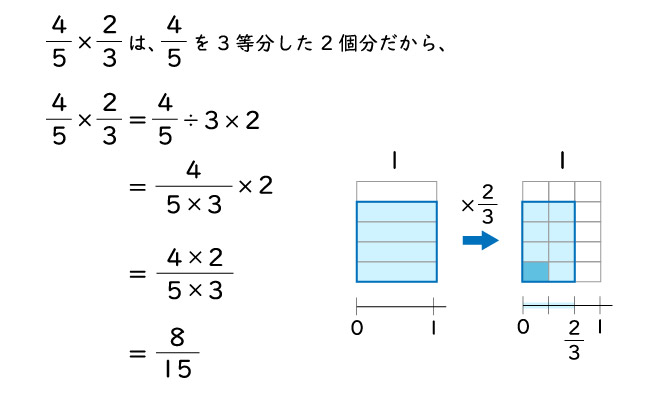
となり、 分母どうし、分子どうしをそれぞれかける というルールが成り立ちます。
$\frac{b}{a} \times \frac{d}{c} = \frac{b \times d}{a \times c}$
分数÷分数は、この中で一番難しいしくみです。
$\frac{3}{5} \div \frac{1}{3}$
の計算のしかたを下の図で考えると、
まずは3分の1を1にするために「3倍」にします。
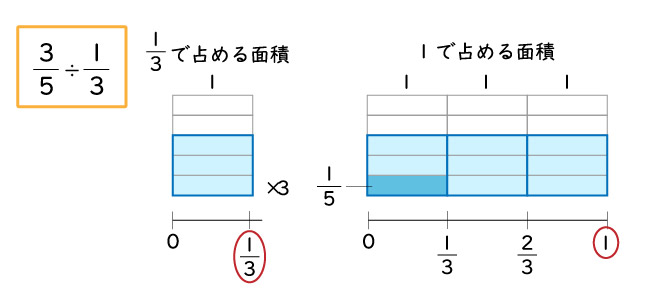
図から、5分の3は5分の9になるのがわかります。
つまり、3分の1を3倍するので、5分の3も3倍することになります。
わる数を1となるように考えて
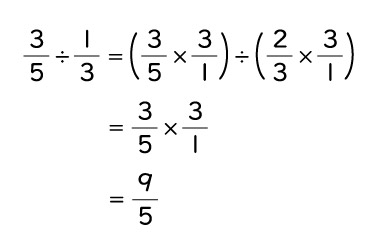
となり、分数のわり算では、わる数の逆算をかけるというルールが成り立ちます。
$\frac{b}{a} \div \frac{d}{c} = \frac{b}{a} \times \frac{c}{d}$
最初はこれらのしくみにとまどうかもしれませんが、分数のかけ算わり算のルールをしっかり覚えて、
整数、小数、分数の四則混合(+、-、×、÷が混じっている)計算がスラスラできるように練習しましょう。
計算エース
| 番号 | 学習内容 | ダウンロード |
| 6-1 | 分数×整数(1) | 問題 解答 |
| 6-2 | 分数×整数(2) | 問題 解答 |
| 6-3 | 分数÷整数(1) | 問題 解答 |
| 6-4 | 分数÷整数(2) | 問題 解答 |
| 6-5 | 分数×整数、分数÷整数 まとめ | 問題 解答 |
| 6ー6 | 分数×分数(1) | 問題 解答 |
| 6-7 | 分数×分数(2) | 問題 解答 |
| 6-8 | 分数×分数(3) | 問題 解答 |
| 6-9 | 分数×分数(4)帯分数がある計算 | 問題 解答 |
| 6-10 | 分数と小数・整数のかけ算(1) | 問題 解答 |
| 6-11 | 分数と小数・整数のかけ算(2) | 問題 解答 |
| 6-12 | 分数×分数 計算のきまり | 問題 解答 |
| 6-13 | 分数÷分数(1) | 問題 解答 |
| 6-14 | 分数÷分数(2) | 問題 解答 |
| 6-15 | 分数÷分数(3)帯分数がある計算 | 問題 解答 |
| 6-16 | 分数÷分数(4)帯分数がある計算 | 問題 解答 |
| 6-17 | 分数÷分数(5)3つの計算 | 問題 解答 |
| 6-18 | 分数÷分数(6)( )のある計算 | 問題 解答 |
| 6-19 | 分数÷分数(7)まとめ | 問題 解答 |
| 6-20 | 分数のかけ算・わり算(1) | 問題 解答 |
| 6-21 | 分数のかけ算・わり算(2) | 問題 解答 |
| 6-22 | 分数のかけ算・わり算(3) | 問題 解答 |
| 6-23 | 分数のかけ算・わり算(4) | 問題 解答 |
| 6-24 | 分数のかけ算・わり算(5) | 問題 解答 |
| 6-25 | わり算を分数になおす計算 | 問題 解答 |
| 6-26 | 四則混合(1) | 問題 解答 |
| 6-27 | 四則混合(2) | 問題 解答 |
| 6-28 | 四則混合(3)計算のきまりをつかって | 問題 解答 |
| 6-29 | 比の値 | 問題 解答 |
| 6-30 | 等しい比(1) | 問題 解答 |
| 6-31 | 等しい比(2) | 問題 解答 |
| 計算エース6年生連番 | 問題 |
復習用まとめ問題
採点方法は減点法です。1問につき5点引いてください。