広島県公立高校入試の小問練習プリントです。
※画像は小問計算1です

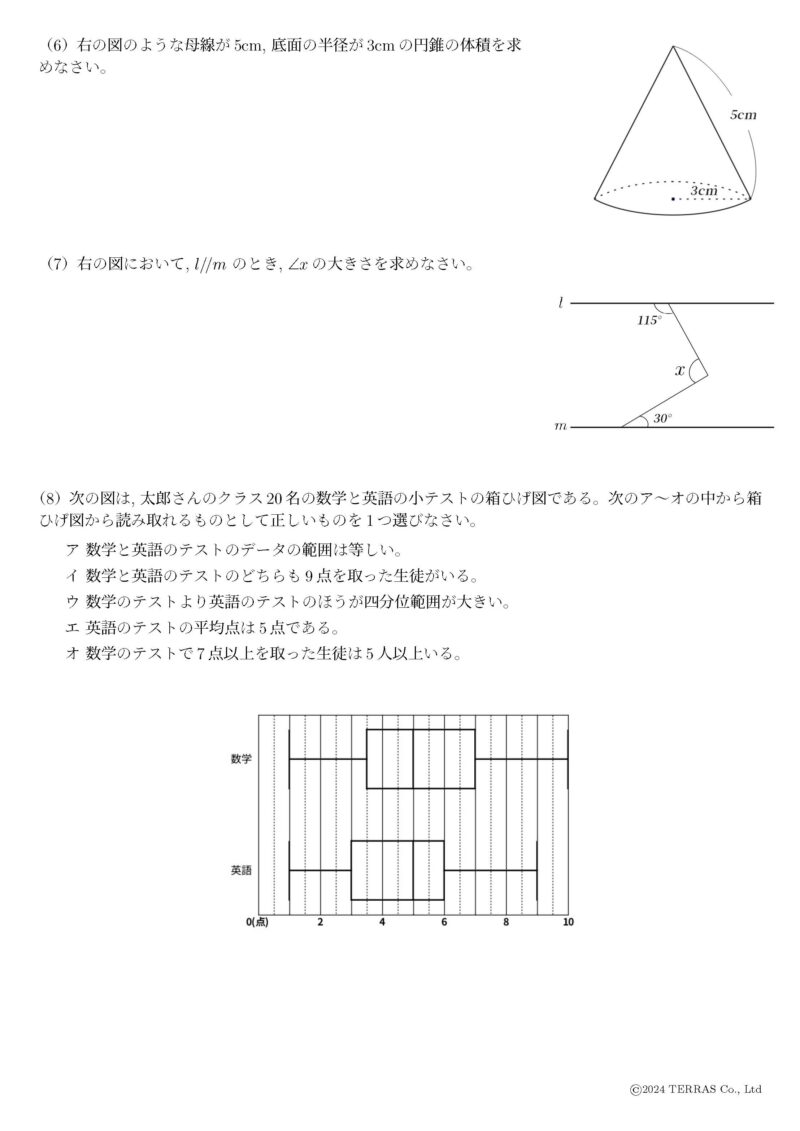

広島県入試傾向
このページでは、広島県公立高校入試(数学)の小問計算問題を中心に傾向、学習ポイント、予想問題を紹介しています。
学力検査日(一般選抜):令和7年2月26日(水)~2月28日(金)
合格発表日(一般選抜):令和7年3月10日(月
時間:50分
配点:50点
問題数:大問6程度
小問計算該当問題:大問1
大問1 難易度★★★☆☆☆☆☆☆☆
各学年の基本計算・小問がメインです。
・正負の数、式の計算
四則演算(足し算・引き算・掛け算・割り算)が混じった計算が出題。
特に除法は頻出なので分数の逆数の仕方などは要練習です。
・平方根の計算
平方根の四則演算の計算が心配な人は練習しておきましょう。
割り算や分数で出題されたときは有理化を忘れないように。
また、展開公式を利用した計算も頻出なので教科書・ワークの問題で確認しておきましょう。
出題例
$(\sqrt{6}+2)(\sqrt{6}-3)$を計算しなさい。 (2024広島)
・方程式
一次方程式、二次方程式ともに様々な問題を解いておくことが大切。
解の公式(二次方程式)も重要公式なので問題を解きながら定着を目指しましょう。
連立方程式も加減法、代入法どちらでも解けるように準備しておきましょう。
解の公式
$ax^{2}+bx+c=0\Rightarrow x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$
出題例
二次方程式$x^{2}+5x-6=0$を解きなさい。 (2021広島)
・図形
各図形の面積や体積、角度を求める公式は必ず覚えておきましょう。
同位角、対頂角、錯角を用いて角度を求める問題は、補助線を引く習慣をつけておくと解きやすいです。
三平方の定理が絡む問題もあるために直角三角形を見つけたら意識するように。
三平方の定理
2辺の長さをa,b,斜辺の長さをcとする直角三角形において、$a^{2}+b^{2}=c^{2}$が成立する。
出題例
1つの外角の大きさが40°である正多角形の辺の数を求めなさい。 (2024広島)
・関数
関数の式を求める問題を教科書やワークで繰り返し解いておきましょう。
・データの活用
度数分布表から、最頻値や中央値、相対度数など各値を求められるようにしておきましょう。
・確率、標本調査
確率はコイン、さいころ、カードの基本問題を解いておきましょう。標本調査は式の作り方が重要なので練習しておきましょう。
【まとめ】
大問1だけでなく、大問2以降も3年間の内容が満遍なく出題されます。全体的な難易度はそこまで高くはないですが、大問数・文章量ともに多いので時間との勝負になります。
偏差値50付近の公立高校や商業・工業などの普通科以外を目指す受験生は大問1はしっかり満点を狙いましょう。大問2以降の小問の中には基本問題が多く含まれているので、そこで点を落とさないように。
進学校を目指す受験生で数学が苦手な場合は、大問1、大問2で満点を目指しましょう。問題数が多いのでわからない問題に時間をかけすぎて最後の問題までの時間を確保ができないことがもったいないので、時間がかかりそうな問題は割り切って次に進むようにしましょう。


