京都府公立高校入試の小問練習プリントです。
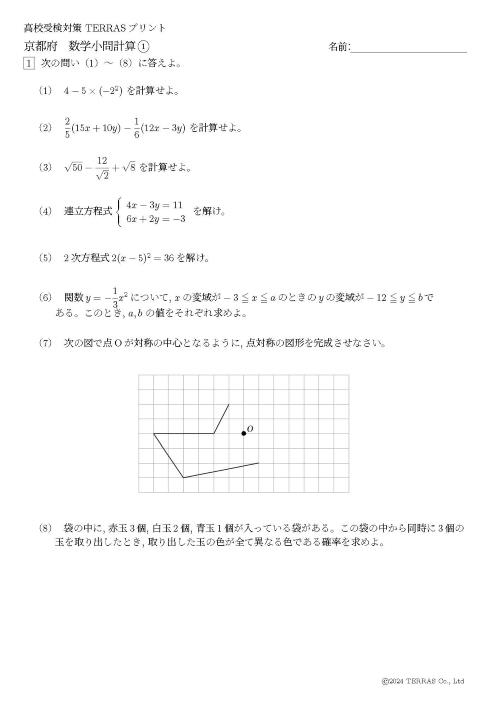
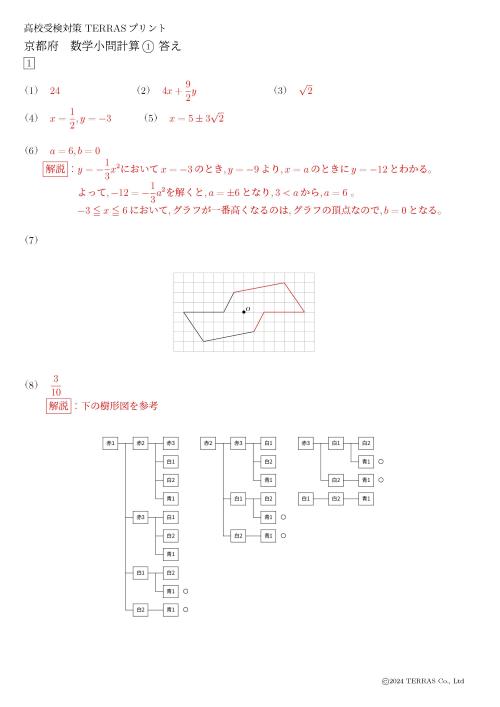
※画像は小問計算1です。
京都府入試傾向
このページでは、京都府公立高校入試中期試験(数学)の小問計算問題を中心に傾向、学習ポイント、予想問題を紹介しています
学力検査日(中期試験):令和7年3月上旬
合格発表日(中期試験):令和7年3月中旬
時間:40分
配点:40点
問題数:大問6程度
小問計算該当問題:大問1
大問1 難易度★★☆☆☆☆☆☆☆☆
学習ポイント:各学年の基本計算から作図まで幅広く出題されます。
・正負の数、式の計算
括弧を外すときや2乗の計算の符号のミスに気を付けよう。
・展開公式の利用
公式を使った計算問題が出題されやすいので4つの公式は覚えておきましょう。因数分解を使って、楽に速く解けるように。
出題例
$x=7,y=-6$のとき、$(x-y)^{2}-10(x-y)+25$の値を求めよ。
4つの展開公式
1. $(x+y)^{2}=x^{2}+2xy+y^{2}$
2. $(x-y)^{2}=x^{2}-2xy+y^{2}$
3. $(x+y)(x-y)=x^{2}-y^{2}$
4. $(x+a)(x+b)=x^{2}+(a+b)x+ab$
・方程式
一次方程式、連立方程式、二次方程式は毎年頻出問題です。どれが出題されてもいいように練習しておきましょう。
・データの分析
2023年度入試までは, 大問1で出題されていたが2024年度からは大問2で出題。大問1で再出題されてもいいように、 箱ひげ図やヒストグラムの読み方や各値の求め方は練習しておきましょう。
・関数
問題文から関数の式を作る練習をしておきましょう。特に、二次関数に関する問題が出題過多傾向です。
変化の割合や変域などの基本問題は解けるように。比例、反比例、一次関数も基本問題は必ず抑えておきましょう。
出題例
$y=\frac{1}{2}x^{2}$について、$x$の値が2から6まで増加するときの変化の割合を求めよ。 (2023京都)
・図形
平行線を利用した線分の長さや円周角を利用した角度を求める問題や対称移動の作図など、広い分野から出題されます。
・確率
コインやさいころなどの基本問題を表や樹形図で解く練習をしておきましょう。
・標本調査
教科書レベルの基本問題で十分対策できます。
【まとめ】
大問1だけでは3~4割の程の配点があるので、とりこぼしが無いように。大問の数は6つと多いですが、基本問題も多く含まれているので、速さも意識して過去問等で練習しましょう。
偏差値50付近の公立高校や商業・工業などの普通科以外を目指す受験生は大問1で点数を稼いで、大問2以降では基本問題を解けるように目指しましょう。大問1以外大問の単元は過去問で傾向がわかるので、自分の得意な単元で点数を積み上げていきましょう。
進学校を目指す受験生で数学が苦手な場合は、まずは大問1で満点が取れるように。京都府の大問1以外のほとんどの大問は小問が2~3個ほどで構成されています。(1)~(3)まである場合、(3)のような最後の問題は時間がかかる可能性が高いため、(1)(2)などの比較的標準的な問題で点数を積み上げて、時間が余れば解けそうな大問の最後の問題にチャレンジしてみよう。

