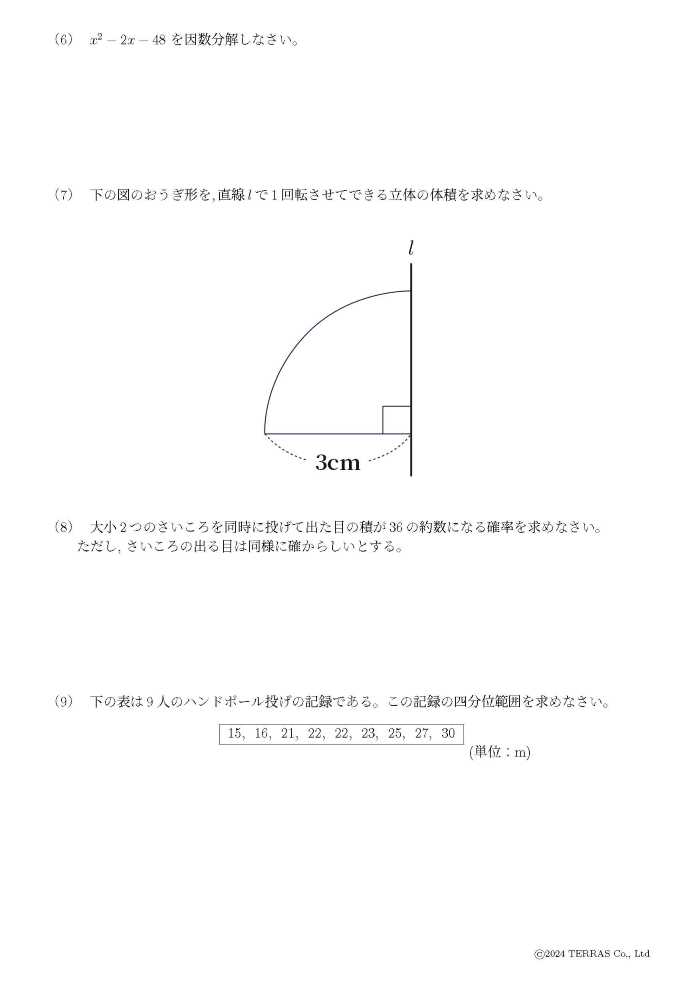
※画像は小問計算1です。


滋賀県入試傾向
このページでは、滋賀県公立高校入試(数学)の小問計算問題を中心に傾向、学習ポイント、予想問題を紹介しています。
学力検査日(一般選抜):令和7年3月5日(水)
合格発表日(一般選抜):令和7年3月12日(水)
時間:50分
配点:100点
問題数:大問4程度
小問計算該当問題:大問1
大問1 難易度★★★☆☆☆☆☆☆☆
各学年の基本計算・問題が出題。傾向はあるものの、幅広く出題されています。
・正負の数
四則演算(足し算・引き算・掛け算・割り算)が混じった計算が出題。分数も出題されるため、通分や逆数の計算も必ずできるようにしておきましょう。計算の順序、符号でミスがないように。
・平方根の計算
平方根の四則演算や展開公式を利用する計算問題を教科書やワークで練習しておきましょう。
4つの展開公式
1. $(x+y)^{2}=x^{2}+2xy+y^{2}$
2. $(x-y)^{2}=x^{2}-2xy+y^{2}$
3. $(x+y)(x-y)=x^{2}-y^{2}$
4. $(x+a)(x+b)=x^{2}+(a+b)x+ab$
出題例
$(\sqrt{2}-\sqrt{3})^{2}+\sqrt{6}$を計算しなさい。 (2022滋賀)
・展開、因数分解
基本問題を中心に色々な式で練習しておきましょう。
・方程式
一次方程式、二次方程式、連立方程式と教科書レベルの問題を解いておきましょう。
二次方程式は解の公式(二次方程式)を使って解けるように。
解の公式
$ax^{2}+bx+c=0\Rightarrow x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$
・図形
立体や回転体の体積や表面積など公式を用いて解けるようにしておきましょう。
・関数
比例・反比例・1次関数・2次関数の式を求める基本問題は確実に解ける準備をしておきましょう。変域の問題はグラフを描きながら解くと、ミスが減ります。
・確率、標本調査
確率はコイン、さいころ、カードの基本問題を解いておきましょう。標本調査は式の作り方が重要なので練習しておきましょう。
出題例
3枚の硬貨を同時に投げるとき, 2枚以上裏となる確率を求めなさい。ただし, 硬貨は, 表と裏のどちらが出ることも同様に確からしいとする。 (2023滋賀)
・データの分析
平均値や中央値、四分位数など各値を箱ひげ図や度数分布表から求められるように。
【まとめ】
大問1だけで全体の4割ほどの点数を占めているので、大問1の正答率が全体の得点のカギとなります。
大問1の出題幅はかなり広いです。毎年この単元が出るとは言い切れないので、過去問を数年分解いて、上記の単元中心に取り組みましょう。
偏差値50付近の公立高校や商業・工業などの普通科以外を目指す受験生は大問1はしっかり満点を狙いましょう。大問2以降では基本問題や得意分野で点を積み重ねていきましょう。大問数が少ない分、分量が多いので、長めの文章題も入試までに練習をしましょう。
進学校を目指す受験生で数学が苦手な場合は、大問1と2で必ず満点をとりましょう。残りの各大問は半分の正解(1つの大問が(1)~(4)まである場合は(1)(2)を解けるようにする)を目指して得点を積み重ねるイメージを持ちましょう。問題数はそこまで多くはないので、大問3と4は最初の小問でミスをすると、それ以降の問題で解き方は合っていても連鎖的に答えが間違いになってしまうので、解きなおし等の時間も考慮しておきましょう。

